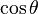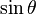Live online human and AI tutoring services
Trigonometric Identity

In trigonometry, the basic relationship between the sine and the cosine is known as the Pythagorean identity:

\sin^2\theta + \cos^2\theta = 1\!

where cos2 θ means (cos(θ))2 and sin2 θ means (sin(θ))2.

Dividing the Pythagorean identity by either cos2 θ or sin2 θ yields two other identities:

1 + \tan^2\theta = \sec^2\theta\quad\text{and}\quad 1 + \cot^2\theta = \csc^2\theta.\! 

Angle-Sum and -Difference Identities

sin(α + β) = sin(α) cos(β) + cos(α) sin(β)

sin(α – β) = sin(α) cos(β) – cos(α) sin(β)

cos(α + β) = cos(α) cos(β) – sin(α) sin(β)

cos(α – β) = cos(α) cos(β) + sin(α) sin(β) 

Using these identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign):
Each trigonometric function in terms of the other five.
in terms of \sin \theta\! \cos \theta\! \tan \theta\! \csc \theta\! \sec \theta\! \cot \theta\!
\sin \theta =\! \sin \theta\ \pm\sqrt{1 - \cos^2 \theta}\! \pm\frac{\tan \theta}{\sqrt{1 + \tan^2 \theta}}\! \frac{1}{\csc \theta}\! \pm\frac{\sqrt{\sec^2 \theta - 1}}{\sec \theta}\! \pm\frac{1}{\sqrt{1 + \cot^2 \theta}}\!
\cos \theta =\! \pm\sqrt{1 - \sin^2\theta}\! \cos \theta\! \pm\frac{1}{\sqrt{1 + \tan^2 \theta}}\! \pm\frac{\sqrt{\csc^2 \theta - 1}}{\csc \theta}\! \frac{1}{\sec \theta}\! \pm\frac{\cot \theta}{\sqrt{1 + \cot^2 \theta}}\!
\tan \theta =\! \pm\frac{\sin \theta}{\sqrt{1 - \sin^2 \theta}}\! \pm\frac{\sqrt{1 - \cos^2 \theta}}{\cos \theta}\! \tan \theta\! \pm\frac{1}{\sqrt{\csc^2 \theta - 1}}\! \pm\sqrt{\sec^2 \theta - 1}\! \frac{1}{\cot \theta}\!
\csc \theta =\! \frac{1}{\sin \theta}\! \pm\frac{1}{\sqrt{1 - \cos^2 \theta}}\! \pm\frac{\sqrt{1 + \tan^2 \theta}}{\tan \theta}\! \csc \theta\! \pm\frac{\sec \theta}{\sqrt{\sec^2 \theta - 1}}\! \pm\sqrt{1 + \cot^2 \theta}\!
\sec \theta =\! \pm\frac{1}{\sqrt{1 - \sin^2 \theta}}\! \frac{1}{\cos \theta}\! \pm\sqrt{1 + \tan^2 \theta}\! \pm\frac{\csc \theta}{\sqrt{\csc^2 \theta - 1}}\! \sec \theta\! \pm\frac{\sqrt{1 + \cot^2 \theta}}{\cot \theta}\!
\cot \theta =\! \pm\frac{\sqrt{1 - \sin^2 \theta}}{\sin \theta}\! \pm\frac{\cos \theta}{\sqrt{1 - \cos^2 \theta}}\! \frac{1}{\tan \theta}\! \pm\sqrt{\csc^2 \theta - 1}\! \pm\frac{1}{\sqrt{\sec^2 \theta - 1}}\! \cot \theta\!