Question 1

In which of the four squares is the ratio of the black area the largest?

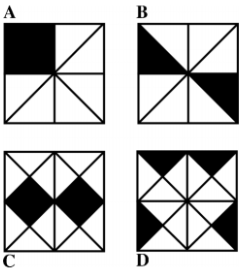
(A) A (B) B (C) C (D) D (E) they are all the same

---

Question 2

Nine cars arrive at a crossroads and drive off as indicated by the arrows.

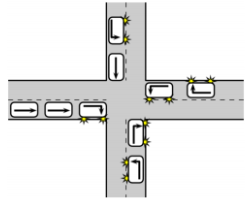
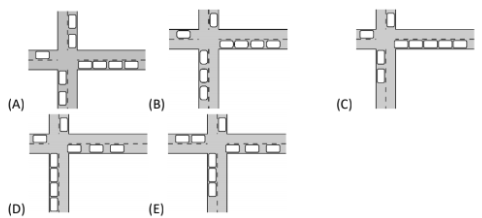
Which figure shows these cars after leaving the crossroads?

---

Question 3

Each of the spots covers one of the numbers 1, 2, 3, 4 or 5 so that both of the calculations following the arrows are correct. What number is covered by the spot with the star?

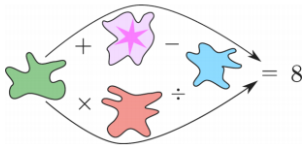
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

---

Question 4

A lion is behind one of the three doors. A sentence is written on each door but only one of the three sentences is true.

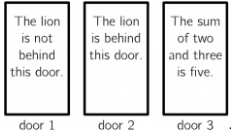
Behind which door is the lion?

(A) Door 1 (B) Door 2 (C) Door 3 (D) All three doors are possible (E) Both door 1 and door 2 are possible

---

Question 5

Two girls, Eva and Olga and three boys, Adam, Isaac and Urban play with a ball. When a girl has the ball, she throws it to the other girl or to a boy. When a boy has the ball, he throws it to another boy but never to the boy from whom he just received it. Eva starts by throwing the ball to Adam. Who will do the fifth throw?

(A) Adam (B) Eva (C) Isaac (D) Olga (E) Urban

---

Question 6

Emily wants to enter a number into each cell of the triangular table. The sum of the numbers in any two cells with a common edge must be the same. She has already entered two numbers. What is the sum of all the numbers in the table?

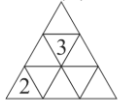
(A) 18 (B) 20 (C) 21 (D) 22 (E) impossible to determine

---

Question 7

On Monday Alexandra shares a picture with 5 friends. For several days everybody who receives the picture, sends it the next day to two friends who haven't seen the picture yet. On which day does the number of people who have seen the picture becomes greater than 100?

 

(A) Wednesday (B) Thursday (C) Friday (D) Saturday (E) Sunday

---

Question 8

The faces of a cube are painted black, white or grey so that opposite faces are of different colour. Which of the following is not a possible net of this cube?

---

Question 9

John does a calculation using the digits A, B, C and D. Which digit is represented by B?

 

(A) 0 (B) 2 (C) 4 (D) 5 (E) 6

---

Question 10

Four ladybugs sit on different cells of a 4x4 grid. One of them is sleeping and does not move. Each time you whistle, the other 3 ladybugs move to a free neighbouring cell. They can move up, down, right or left but they are not allowed to go back to the cell they just came from. Which of the following images might show the result after the fourth whistle?

---

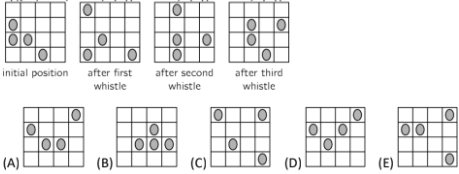
Question 11

From the list 3, 5, 2, 6, 1, 4, 7 Masha chose 3 different numbers whose sum is 8. From the same list Dasha chose 3 different numbers whose sum is 7. How many common numbers have been chosen by both girls?

 

(A) none (B) 1 (C) 2 (D) 3 (E) impossible to determine

---

Question 12

Five balls weigh 30 g, 50 g, 50 g, 50 g and 80 g, respectively.

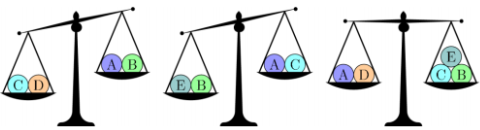
Which ball weighs 30 g?

 

(A) A (B) B (C) C (D) D (E) E

---

Question 13

If A, B, C are distinct digits, then the largest possible 6-digit number written using 3 digits A, 2 digits B, and 1 digit C cannot be equal to

 

(A) AAABBC (B) CAAABB (C) BBAAAC (D) AAABCB (E) AAACBB

---

Question 14

The sum of the ages of Kate and her mother is 36, and the sum of the ages of her mother and her granny is 81. How old was her granny when Kate was born?

 

(A) 28 (B) 38 (C) 45 (D) 53 (E) 56

---

Question 15

Nick wants to arrange the numbers 2, 3, 4, ..., 10 into several groups such that the sum of the numbers in each group is the same. What is the largest number of groups he can get?

 

(A) 2 (B) 3 (C) 4 (D) 6 (E) other answer

---

Question 16

Peter saw an 8 cm wide wooden shelf into 9 parts. One piece was a square, the rest were rectangles. Then he put all the pieces together as shown in the picture. How long was the shelf?

(A) 150 cm (B) 168 cm (C) 196 cm (D) 200 cm (E) 232 cm

---

Question 17

Write 0 or 1 in each cell of the 5x5 table such that each 2x2 square of the 5x5 table contains exactly 3 equal numbers. What is the largest possible sum of all the numbers in the table?

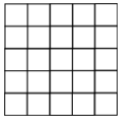
(A) 22 (B) 21 (C) 20 (D) 19 (E) 18

---

Question 18

14 people are seated at a round table. Each person is either a liar or tells the truth. Everybody says: "Both my neighbours are liars". What is the maximum number of liars at the table?

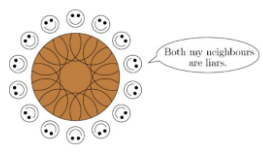
(A) 7 (B) 8 (C) 9 (D) 10 (E) 14

---

Question 19

There are eight domino tiles on the table (pic 1). One half of one tile is covered. The 8 tiles can be arranged into a 4x4 square (pic 2), so that the number of dots in each row and column is the same.

How many dots are on the covered part ?

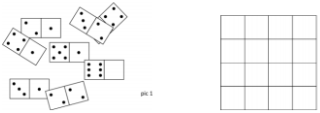
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

---

Question 20

Write the numbers 3, 4, 5, 6, 7, 8 and 9 in the seven circles to obtain equal sums along each of the three lines. What is the sum of all possible numbers replacing the question mark?

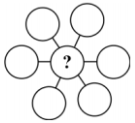
(A) 3 (B) 6 (C) 9 (D) 12 (E) 18

---

Question 21

The five cards with the numbers from 1 to 5 lie in a horizontal row (see the figure). Per move, any two cards may be interchanged. Find the smallest number of the moves required to arrange all cards in increasing order?

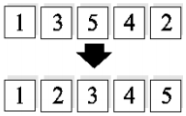
(A) 1 (B) 2 (C) 3 (D) 4

---

Question 22

How many hours are there in half of a third of a quarter of a day?

(A) 1/3 (B) 1/2 (C) 1 (D) 2

---

Question 23

Raza needs 40 minutes to walk from home to the sea by foot and to return home on an elephant. When he rides both ways on an elephant, the journey takes 32 minutes.

How long would the journey last, if he would walk both directions?

 

(A) 36 minutes (B) 42 minutes (C) 46 minutes (D) 48 minutes

---

Question 24

If the sum of five consecutive positive integers is 2005, then the largest of these numbers is

(A) 401 (B) 403 (C) 405 (D) 2001

---

Question 25

How many different factors (including 1 and 100) does 100 have?

(A) 6 (B) 7 (C) 8 (D) 9

---

Question 26

If you count the number of all possible triangles and the number of all possible squares in the picture how many more triangles than squares do you find?

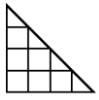
(A) the same quantity (B) 1 (C) 2 (D) 3

---

Question 27

Which of equalities means that m makes 30 % from k?

 

(A) 10m ? 3k = 0 (B) 3m ? 10k = 0 (C) 7m ? 10k = 0 (D) 7m ? 3k = 0

---

Question 28

If you fold up the net on the right, which of these cubes can you make?

---

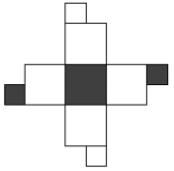
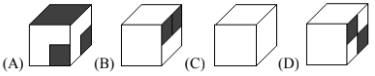
Question 29

Different figures represent the different digits. Find the digit corresponding to the square.

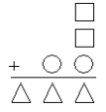
(A) 9 (B) 8 (C) 7 (D) 6

---

Question 30

In a trunk there are 5 chests, in each chest there are 3 boxes, and in each box there are 10 gold coins. The trunk, the chests, and the boxes are locked. How many locks must be opened in order to get 50 coins?

 

(A) 5 (B) 7 (C) 8 (D) 9

---

Question 31

A caterpillar starts from his home and move directly on a ground, turning after each hour at 90? to the left or to the right. In the first hour he moved 1 m, in the second hour 2 m, and so on. At what

minimum distance from his home the caterpillar would be after six hours traveling?

 

(A) 0 m (B) 1 m (C) 1.5 m (D) 2.5 m

---

Question 32

The sum of ten distinct positive numbers is 100. The largest of these numbers can be:

 

(A) 10 (B) 13 (C) 55 (D) 60