Question 1
Which of the following figures cannot be formed by gluing these two identical squares of paper together?
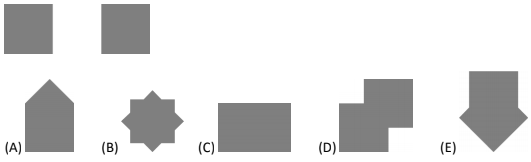
Question 2
Mary, Ann, and Nata work in a kindergarten. Each day from Monday to Friday exactly two of them come to work. Mary works 3 days per week and Ann works 4 days per week. How many days per week does Nata work?
(A) 1 (B) 2 (C) 3 (D) 4 (E) 5
Question 3
Five squirrels A, B, C, D, and E are sitting on the line. They pick 6 nuts marked by crosses. At one moment the squirrels start running to the nearest nut at the same speed. As soon as a squirrel picks a nut it starts running to the next closest nut. Which squirrel will get two nuts?
(A) A (B) B (C) C (D) D (E) E
Question 4
There are 30 students in a class. They sit by pairs so that each boy is sitting with a girl, and exactly half of the girls are sitting with a boy. How many boys are there in the class?
(A) 25 (B) 20 (C) 15 (D) 10 (E) 5
Question 5
The number 2581953764 is written on a strip of paper. John cuts the strip 2 times and gets 3 numbers. Then he adds these 3 numbers. Which is the smallest possible sum he can get?
(A) 2675 (B) 2975 (C) 2978 (D) 4217 (E) 4298
Question 6
Bart is getting his hair cut. When he looks in the mirror the clock looks like the one shown. What would he have seen if he had looked in the mirror ten minutes earlier?
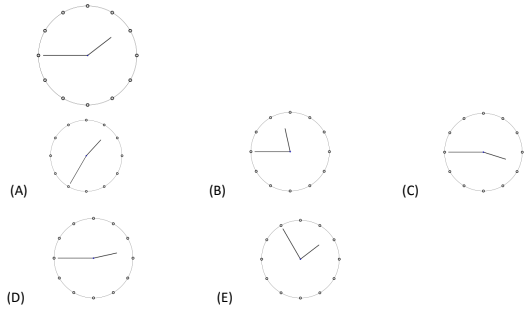
Question 7
Grandmother bought enough cat food for her four cats to last for 12 days. On her way home she brought back two stray cats. If she gives each cat the same amount of food every day, how many days will the cat food last?
(A) 8 (B) 7 (C) 6 (D) 5 (E) 4
Question 8
Each letter in BENJAMIN represents one of the digits 1, 2, 3, 4, 5, 6 or 7. Different letters represent different digits. The number BENJAMIN is odd and divisible by 3. Which digit corresponds to N?
(A) 1 (B) 2 (C) 3 (D) 5 (E) 7
Question 9
Tim, Tom and Jim are triplets, while their brother Carl is 3 years younger. Which of the following numbers could be the sum of the ages of the four brothers?
(A) 53 (B) 54 (C) 56 (D) 59 (E) 60
Question 10
The perimeter of the rectangle ABCD is 30 cm. Three other rectangles are placed so that their centres are at the points A, B and D (see the figure). The sum of their perimeters is 20 cm. What is he total length of the thick line?
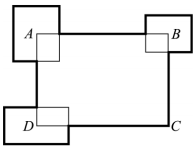
(A) 50 cm (B) 45 cm (C) 40 cm (D) 35 cm (E) impossible to determine
Question 11
Anna folds a round sheet of paper at the middle. Then she folds it once more and then one last time.
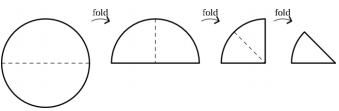
In the end Anna cuts the folded paper along the marked line:
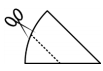
What is the shape of the middle part of the paper when unfolded?
Question 12
Richard writes down all the numbers with the following properties:
a. the first digit is 1,
b. each of the following digits is at least as big as the one before it,
c. the sum of the digits is 5.
How many numbers does he write?
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
Question 13
What is the greatest number of shapes of the form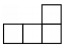 
that can be cut out from a 5 ? 5 square?
(A) 2 (B) 4 (C) 5 (D) 6 ( E) 7
Question 14
Luigi started a small restaurant. His friend Giacomo gave him some square tables and chairs. If he uses all the tables as single tables with 4 chairs each, he would need 6 more chairs. If he uses all the tables as double tables with 6 chairs each, he would have 4 chairs left over. How many tables did Luigi get from Giacomo?
(A) 8 (B) 10 (C) 12 (D) 14 (E) 16
Question 15
Clara wants to construct a big triangle using identical small triangular tiles. She has already put some tiles together as shown in the picture. How many tiles does she need to complete a triangle?
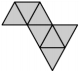
(A) 5 (B) 9 (C) 12 (D) 15 (E) 18
Question 16
A big cube was built from 8 identical small cubes, some black ones and some white ones. Five faces of the big cube are:
What does the sixth face of the big cube look like?
Question 17
Kirsten wrote numbers in 5 of the 10 circles as shown in the figure. She wants to write a number in each of the remaining 5 circles such that the sums of the 3 numbers along each side of the pentagon are equal. Which number will she have to write in the circle marked by X?
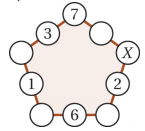
(A) 7 (B) 8 (C) 11 (D) 13 (E) 15
Question 18
The symbols 
and represent 3 different digits.
If you add the digits of the 3-digit number 
, the result is the 2-digit number 
.
If you add the digits of the 2-digit number 
, you find the 1-digit number 
.
Which digit does 
represent?
(A) 4 (B) 5 (C) 6 (D) 8 (E) 9
Question 19
A little Kangaroo is playing with his calculator. He starts with the number 12. He multiplies or divides the number by 2 or 3 (if possible) 60 times in a row. Which of the following results cannot be obtained?
(A) 12 (B) 18 (C) 36 (D) 72 (E) 108
Question 20
Two 3-digit numbers have all their 6 digits distinct. The first digit of the second number is twice the last digit of the first number. What is the smallest possible sum of two such numbers?
(A) 552 (B) 546 (C) 301 (D) 535 (E) 537
Question 21
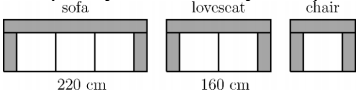
The Modern Furniture store is selling sofas, loveseats(lovecat), and chairs made from identical modular pieces as shown in the picture. Including the armrests, the width of the sofa is 220 cm and the width of the loveseat is 160 cm. What is the width of the chair?
(A) 60 cm (B) 80 cm (C) 90 cm (D) 100 cm (E) 120 cm
Question 22
The 5 keys fit the 5 padlocks. The numbers on the keys refer to the letters on the padlocks. What is written on the last key?
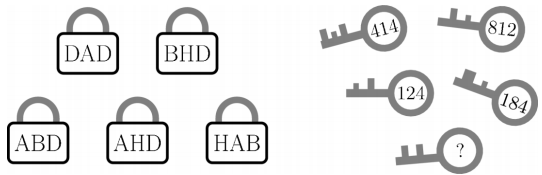
A) 382 (B) 282 (C) 284 (D) 823 (E) 824
Question 23
Tom writes all the numbers from 1 to 20 in a row and obtains the 31-digit number 1234567891011121314151617181920. Then he deletes 24 of the 31 digits such that the remaining number is as large as possible.
Which number does he get?
(A) 9671819 (B) 9567892 (C) 9781920 (D) 9912345 (E) 9818192
Question 24
Morten wants to put the construction into a regular box. Which of the following boxes is the smallest he can use?
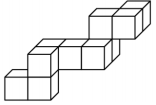
(A) 3 x 3 x 4 (B) 3 x 5 x 5 (C) 3 x 4 x 5 (D) 4 x 4 x 4 (E) 4 x 4 x 5
Question 25
When we add the numbers in each row and along the columns we get the results shown. Which statement is true?
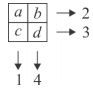
(A) a is equal to d (B) b is equal to c (C) a is greater than d (D) a is less than d (E) c is greater than b
Question 26
Peter went hiking in the mountains for 5 days. He started on Monday and his last trip was on Friday. Each day he walked 2 km more than the day before. When the tour was over, his total distance was 70 km. What distance did Peter walk on Thursday?
(A) 12 km (B) 13 km (C) 14 km (D) 15 km (E) 16 km
Question 27
There is a picture of a kangaroo in the first triangle. Dotted lines act as mirrors. The first 2 reflections are shown. What does the reflection look like in the shaded triangle?
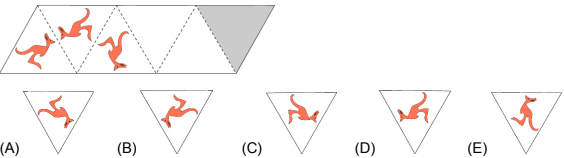
Question 28
Numbers are placed in the cells of the 4 ? 4 square shown in the picture. Mary finds the 2 ? 2 square where the sum of the numbers in the four cells is the largest. What is that sum?
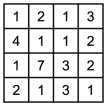
(A) 11 (B) 12 (C) 13 (D) 14 (E) 15
Question 29
Rafael has three squares. The first one has side length 2 cm. The second one has side length 4 cm and a vertex is placed in the centre of the first square. The last one has side length 6 cm and a vertex is placed in the centre of the second square, as shown in the picture. What is the area of the figure?
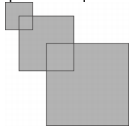
(A) 32 cm2
(B) 51 cm2
(C) 27 cm2
(D) 16 cm2
(E) 6 cm2
Question 30
Four players scored goals in a handball match. All of them scored a different number of goals. Among the four Mike was the one who scored the least number of goals. The other three have scored 20 goals in total.
What is the largest number of goals Mike could have scored?
(A) 2 (B) 3 (C) 4 (D) 5 (E) 6
Question 31
A bar consists of 2 grey cubes and 1 white cube glued together as shown in the figure. Which figure can be built from 9 such bars?
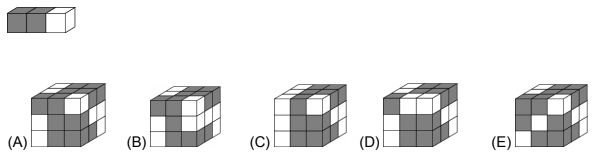
Question 32
The numbers 1, 2, 3, 4, and 5 have to be written in the five cells in the figure in the following way: if a number is just below another number, it has to be greater. If a number is just to the right of another number, it has to be greater.
In how many ways can this be done?
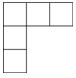
(A) 3 (B) 4 (C) 5 (D) 6 (E) 8
Question 33
8 kangaroos stood in a line as shown in the diagram. At some point, two kangaroos standing side by side and facing each other exchanged places by jumping past each other. This was repeated until no further jumps were possible. How many exchanges were made?
(A) 2 (B) 10 (C) 12 (D) 13 (E) 16
Question 34
What number must be subtracted from −17 to obtain −33?
(A) −50 (B) −16 (C) 16 (D) 40 (E) 50
Question 35
The square floor in the picture is covered by triangular and square tiles in grey and white. At least how many tiles must be swapped such that the pattern looks the same from each of the four directions shown?
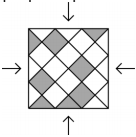
(A) Three triangles, one square
(B) One triangle, three squares
(C) One triangle, one square
(D) Three triangles, three squares
(E) Three triangles, two squares
Question 36
A bag contains only red marbles and green marbles. For any 5 marbles we pick, at least one is red; for any 6 marbles we pick, at least one is green. What is the largest number of marbles that the bag can contain?
(A) 11 (B) 10 (C) 9 (D) 8 (E) 7
Question 37
Ala likes even numbers, Beata likes numbers divisible by 3, Celina likes numbers divisible by 5. Each of these three girls went separately to a basket containing 8 balls with numbers written on them, and took all the balls with numbers she likes. It turned out that Ala collected balls with numbers 32 and 52 , Beata 24, 33 and 45 , Celina 20, 25 and 35. In what order did the girls approach the basket?
(A) Ala, Celina, Beata
(B) Celina, Beata, Ala
(C) Beata, Ala, Celina
(D) Beata, Celina, Ala
(E) Celina, Ala, Beata
Question 38
John wants to write a natural number in each box in the diagram such that each number above the bottom row is the sum of the two numbers in the boxes immediately underneath. What is the largest number of odd numbers that John can write?
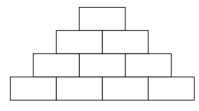
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
Question 39
Julia has four different coloured pencils and wants to use some or all of them to paint the map of an island divided into four nations, as in the picture. If the map of two nations with a common border cannot have the same colour, in how many ways can she colour the map of the island?
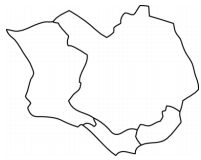
(A) 12 (B) 18 (C) 24 (D) 36 (E) 48
Question 40
In each cell of a 6 ? 6 board there is a lamp. We say that two lamps in this board are neighbours if they lie in cells with a common side. Initially some lamps are lit and, each minute, every lamp having at least two lit neighbouring lamps is lit. What is theinimum number of lamps that need to be lit initially, in order to ensure that, at some time, all lamps will be lit?
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
Answer Keys
Question 1: A
Question 2: C
Question 3: C
Question 4: D
Question 5: B
Question 6: E
Question 7: A
Question 8: D
Question 9: A
Question 10: C
Question 11: D
Question 12: B
Question 13: D
Question 14: B
Question 15: B
Question 16: D
Question 17: D
Question 18: E
Question 19: C
Question 20: E
Question 21: D
Question 22: C
Question 23: C
Question 24: C
Question 25: D
Question 26: E
Question 27: E
Question 28: D
Question 29: B
Question 30: C
Question 31: A
Question 32: D
Question 33: D
Question 35: C
Question 36: C
Question 37: D
Question 38: D
Question 39: E
Question 40: C